Two variations of the 2-D Logarithmic (
TDL) search were implemented and used on the three test sequences. TDL-N halved the step size only when the centre of a stage was the point with minimum distortion. In addition to halving the step size under these conditions, TDL-X also halved the step size if the point of minimum distortion was at the boundary of the search area. Both variations began with step sizes of (2
d+1) div 4.
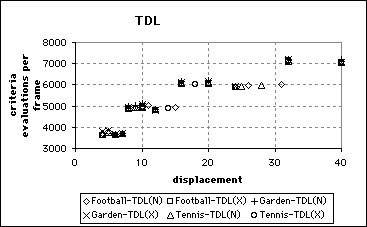
The results graphed in Figure 5.8 suggest that the computational complexity of the TDL search was largely independent of the sequence coded. As the maximum allowable displacement increased, the average number of matching criteria evaluations per frame increased in a step fashion. This would suggest that for any displacement of the form 2
n+
q< 2
n+1 (where
n and
q are integers) the value of
q can be maximised at no cost. For example a TDL search with maximum displacement of ±15 pixels is likely to require about the same number of criteria evaluations as a search with a displacement of ±8 pixels. Similarly the decision to increase the displacement from ±15 to ±16 pixels should be carefully considered. The TDL search’s step behaviour should be considered when choosing the displacement parameter for a search.
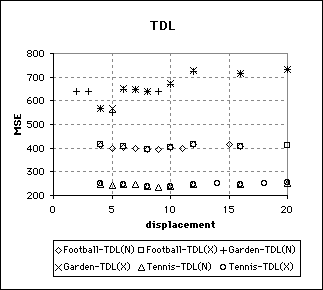
The two variants of the TDL search that were implemented exhibited very similar behaviour. Invariably, however, the TDL-X variation evaluated marginally fewer candidate blocks which resulted in slightly higher MSE values.
The MSE values were of course different for each sequence, since some sequences were easier to code than others. Unlike the exhaustive search the MSE did not decrease indefinitely as the maximum displacement increased (See graph above). This was because the TDL search is susceptible to local minima when the maximum displacement used is large compared to the actual motion in the scene.
For small displacements on the Football and Tennis sequences the MSE decreased as the displacement was increased, just as was the case with the exhaustive search. Starting with a displacement of ±10 pixels the MSE began to increase. This increase was most likely a consequence of the displacement being considerably greater than that required to account for the actual motion in the sequence. If the displacement used by the BMA is very large then the positions examined in the early stages of the algorithm might not be in the neighbourhood of the global minimum. This can result in the algorithm converging on a local minimum rather than the global.
This behaviour gives rise to the concept of an
operative range. The operative range of a block matching algorithm is a maximum displacement value beyond which the BMA fails to work productively. Determining the operative range can be difficult. If the MSE begins to increase with the maximum allowable displacement then it is likely that the BMA is operating outside of its range. The operative range is primarily a function of the motion in a frame. If objects move large distances between frames then the operative range will be greater than if the objects moved very short distances.
The concept of the operative range is useful when choosing parameters for video compressors. One might mistakenly assume that increasing the maximum allowable displacement increases the quality of the matches, as is the case with the exhaustive search. It is known that bad matches can result when the actual motion of blocks exceeds the maximum displacement of a BMA. The results of these experiments show however that arbitrary large displacements might not only fail to solve this problem, but can result in even worse matches being found.
This goes a long way to explaining the behaviour of the algorithm when coding the Garden sequence. The operative range of the TDL was much lower for the Garden sequence than for the other two sequences and the MSE began to rise beyond ± 5 pixels.
That the operative range is lower for the Garden sequence does not completely explain the behaviour of the algorithm. The increase in MSE was much more dramatic than for the Football and Tennis sequence. This may be due to the large amount of repeated detail in the Garden sequence making it more susceptible to convergence on local minima.
The Garden sequence differs from the other two sequences in one other and very important way. Although the distance each block of the Garden sequence moves is small, the number of moving blocks is very large. The football and Tennis sequences have stationary backgrounds which result in some motionless blocks. In the Garden sequence every block is moving. Thus the increase in error resulting from local minima and excessive search areas is compounded by the fact that it applies to a great many blocks.
[return to
Experiments and Conclusions]
© Colin E. Manning 1996