Cross Search Algorithm
The cross search algorithm, introduced by Ghanbari in 1990, is similar in many ways to Jain & Jain’s 2-D logarithmic search [
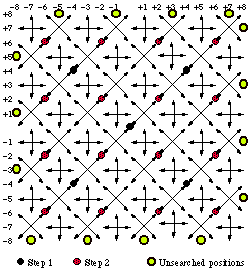
Ghan90]. In all but the last stage, however, the four search points form the edges of a saltire cross (X) rather than a Greek cross (+) as used in the TDL search. At each stage the step size is halved, until the final stage when it is equal to one. At the final stage, however, the end points of a Greek cross (+) are used to search areas centred around the top-right and bottom-left corners of the previous stage, and a saltire cross (X) is used to search areas centred around the top-left and bottom-right corners of the previous stage.
Some points in the search space are never evaluated as potential locations of matching blocks. In general, one quarter of all the positions at the search area boundary are not considered by the Cross Search Algorithm. This problem can result in the effective search area being one position less in all four directions.
The last stages of the CSA for an 8 by 8 pixel search area. The centres of the first and second stages are marked. The centres of the penultimate stage occur where arrows cross and the resulting search points for the last step are indicated by arrows.